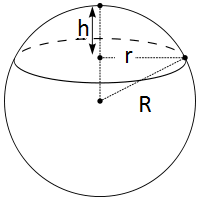
A spherical cap is a three-dimensional geometric shape that is formed by slicing off the top portion of a sphere with a plane. The volume of a spherical cap represents the space enclosed by its curved surface and is calculated by considering the height of the cap and the radius of the sphere.
To determine the volume of a spherical cap, we use the formula V = (1/3)πh²(3r – h), where V represents the volume, h is the height of the cap, and r denotes the radius of the sphere. Here, π (pi) is a mathematical constant approximately equal to 3.14159.
By substituting the values of the height and radius into the formula, we can calculate the volume of the spherical cap. For example, let’s consider a spherical cap with a height of 4 units and a sphere radius of 6 units:
V = (1/3)π(4)²(3(6) – 4)
= (1/3)π(16)(14)
= (224/3)π cubic units
Hence, the volume of the spherical cap with a height of 4 units and a sphere radius of 6 units is approximately 234.57205 cubic units.