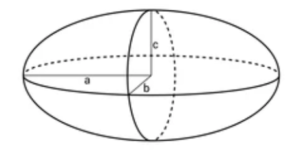
An ellipsoid is a three-dimensional shape that looks like a stretched or squashed sphere. To calculate its volume, we need to know the lengths of its three axes: a, b, and c.
The formula to find the volume of an ellipsoid is V = (4/3)πabc, where V represents the volume, a is the length of the first axis, b is the length of the second axis, and c is the length of the third axis. π (pi) is a number approximately equal to 3.14159.
By plugging in the values of the axes into the formula, we can calculate the volume of the ellipsoid. For example, let’s say we have an ellipsoid with axis lengths of 4 units, 6 units, and 8 units for a, b, and c, respectively:
V = (4/3)π(4)(6)(8)
= (4/3)π(192)
= 256π cubic units
Therefore, the volume of the ellipsoid with axis lengths a = 4 units, b = 6 units, and c = 8 units is approximately 804.24772 cubic units.