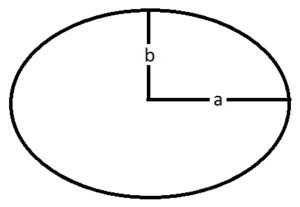
The area of an ellipse is a fundamental geometric property, signifying the extent of the space enclosed within its curved boundary. An ellipse is a closed curve with two main axes – the major axis and the minor axis – that are perpendicular to each other.
To calculate the area of an ellipse, you can use the following formula:
Area = π * a * b
In this formula, ‘a’ represents the length of the semi-major axis, and ‘b’ represents the length of the semi-minor axis.
By applying the formula mentioned above, you can determine the precise area of the ellipse. The product of π and the lengths of the semi-major and semi-minor axes provides the total area.
Understanding the area of an ellipse is vital in various fields, including physics, engineering, and astronomy. It plays a significant role in estimating surface areas, designing ellipsoidal objects, and solving geometric problems.