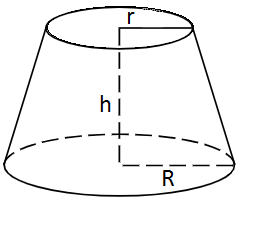
A conical frustum is a three-dimensional geometric shape that is formed by cutting a cone with a plane parallel to its base, resulting in a truncated cone-like structure. The volume of a conical frustum represents the space enclosed by its curved surface. To calculate the volume, we need to know the radii of the two circular bases and the height of the frustum.
The formula for calculating the volume of a conical frustum is V = (1/3)πh(r² + R² + rR), where V represents the volume, h is the height of the frustum, R is the radius of the larger base, and r is the radius of the smaller base. Here, π (pi) is a mathematical constant approximately equal to 3.14159.
Let’s consider an example to better understand this concept. Suppose we have a conical frustum with a larger base radius of 7 units, a smaller base radius of 3 units, and a height of 5 units:
V = (1/3)π(5)(7² + 3² + 7 × 3)
= (1/3)π(5)(49 + 9 + 21)
= (1/3)π(5)(79)
≈ 413.64303 cubic units
Therefore, the volume of the conical frustum with a larger base radius of 7 units, a smaller base radius of 3 units, and a height of 5 units is approximately 413.64303 cubic units.